Schrödinger macskájának példázata közismert: amíg ki nem nyitjuk a dobozt, nem derül ki, hogy a macska él-e vagy meghalt. A történet a kétállapotú kvantumrendszerek (azaz qubitek) paradox működését illusztrálja, makroszkopikussá nagyítja a kvantumjelenséget*. Amíg el nem végzünk egy mérést, addig egy rendszer a két állapot valamiféle keverékében van, a mérés hatására azonban beugrik a két állapot egyikébe. De milyen állapotban van a kvantummacska, amíg nem nyitjuk ki a dobozt? Ez a kérdés, amint az állapotnak a mérés hatására bekövetkező összeomlása is, fizikai-filozófiai értelemben megoldatlan probléma, azonban a jelenség modellezésére használt matematikai képet nem is olyan nehéz megérteni. Ez a Hopf-fibrálás, mely egy négydimenziós mintázat háromdimenziós vetülete.
Ha már jól behipnotizáltuk magunkat a három csúszka segítségével, nézzük meg, mit is látunk! De előbb jöjjön egy kis személyes történeti bevezető.
Jó két éve javasolta Horváth Bence a 444-től, hogy írjak egy cikket a kedvenc képletemről. Hogy mi az, azt egyből tudtam, hiszem kitaláltam már ez előtt, amikor egy MateMorfózis szeánsz alkalmával megkért a Kék Ló egyik pultban dolgozó munkatársa, hogy írjam fel a kezére. Tehát ekkor derült ki, hogy a kedvenc képletem a Hopf-fibrálás. Jól ki is fundáltam akkor a koncepciót. Volt egy félbemaradt áltudományos dalelemző sorozat itt a blogon, ide szántam a cikk hosszabb verzióját az időközben megjelent (halál;orgazmus): Dinamikus Meditáció lemezhez kapcsolódva, melynek borítóján épp a Hopf-nyaláb látható. Gressai Ferdivel gézből készítettük el a Hopf-köröket a dalszövegekben többször említett titokzatos eredetű szétfutó és becsavaró szálak szimbólumaként. Egyébként a lemezborítón matematikai értelemben van egy hiba, aki azt megtalálja, kap egy példányt a lemezből feltéve, hogy azt is megtalálja, hová tettük a fennmaradó példányokat.
Szóval kettőt egy csapásra, ez volt a terv, és ezzel fejeztem volna be az Áltudományos verselemző sorozatot. Azóta (halál;orgazmus) már inkább nincs, mint van, ha csak e két létállapot közül lehet választani, de valójában inkább szuperpozícióban van, mint a macska. A Hopf-fibrálás pedig aktuálisabbá vált számomra, mint valaha. Egy BME-s elméleti fizikus kutatócsoporthoz volt szerencsém csatlakozni, és megállapítottam, hogy az előző mondatban a nem igazán működő régebbi zenekaromról tett vicceskedő megállapítás is szorosan összefügg a Hopf-fibrálással, mivel utóbbi a kétállapotú kvantumrendszerek, illetve a kvantuminformáció alapegységét képező qubit matematikai modelljét foglalja magában. Az Kronoszinklasztikus Infundibulum elnevezésű újabb bandám fénytechnikusai, Matyi&Matyi pedig Hopf-fibrálást vetítettek a koncertjeinkhez, és egyikük gyanútlanul meg is kérdezte, ismerem-e ezt az ábrát. Így az újabb zenekaromban is visszatért a téma továbbá ismerős fizikus körökben is előkerült, itt volt hát az ideje leírni, mi is ez! Végül sem Qubit, sem 444 cikk nem lett a dologból de... Az Érintő folyóiratban leírtam részletesen a Hopf-fibrálás matematikai kontextusát, ez a poszt pedig a Bodnár Józsi kollégám és barátom által készített GeoGebra animációt kísérő informális mese az élőhalott cicusról. Szóval!
A klasszikus digitális információ alapegysége a bit, amelynek értéke lehet 0 vagy 1. Fizikailag ezt egy kétállapotú rendszer valósítja meg, praktikusan egy áramkörben átfolyik az áram (1) vagy sem (0). A kvantuminformatikában a bit megfelelője a qbit, egy kétállású kvantumrendszer. A qubiteknek végtelen sok lehetséges állapotuk van, amíg meg nem mérjük őket. Schrödinger macskája egy gondolatkísérlet ennek illusztrálására: nem tudni, hogy él-e vagy meghalt, amíg fel nem nyitjuk a dobozt.
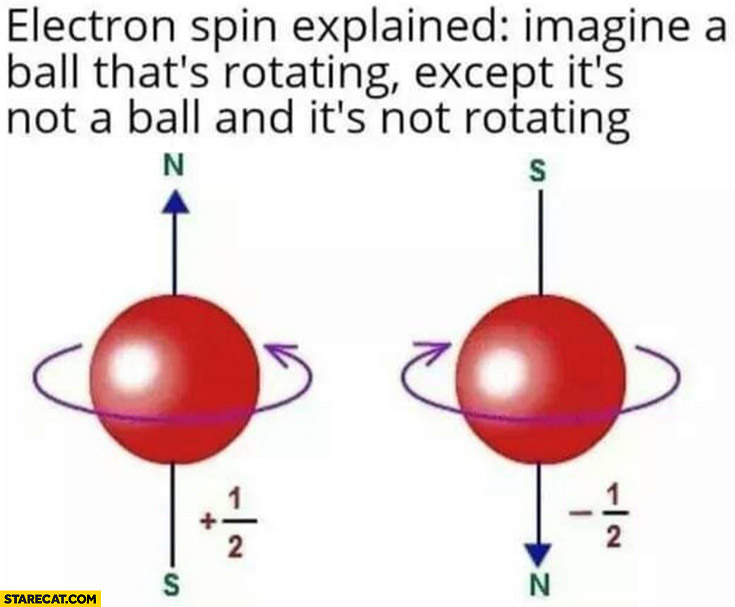
A méltán elhíresült cicus után a leghíresebb kétállapotú kvantumrendzser az elektron spinje. Egy elektron spinje állhat egy adott irányban felfelé vagy lefelé, de hogy mi ennek a jelentése, az elég zavaros, amint az alábbi mém mutatja: Képzelj el egy golyót, ami pörög. Csak ez nem golyó és nem pörög. (A nempörgő pörgőssel a hamarosan megjelenő Új világok teremtése című könyvemben fogok foglalkozni egy alfejezet erejéig.) A spin mibenlétére a matematikailag tökéletes válasz a Hopf-fibrálás, ami persze egy elektron tényleges elképzeléséhez nem sokat segít, csak a lehetséges állapotok leírásához...
Az elektron spinje úgy viselkedik, mint a Schrödinger macskája: a mérésig a kétféle mérés utáni állapot valamiféle keverékében van. A rendszer állapotát első megközelítésben egy valószínűség írja le, pl. 30% annak valószínűsége, hogy a macska még él (az elektron spinje felfelé áll), és 70% annak, hogy meghalt (a spin lefelé áll). Ha megmérjük, rákérdezünk az állapotára, akkor ugrik csak be a 0 vagy 1 állapotok valamelyikébe.
Azonban egy kvantumrendszer a valószínűségeknél jóval több információt hordoz, a kölcsönhatások matematikai leírásához ezekre is szükség van. A GeoGebra animáción a három csúszkával a rendszer teljes állapotát állítgathatjuk. Egy állapot megadásához két mutatót kell beállítanunk, amik foroghatnak egymástól függetlenül, és megnyúlhatnak vagy megrövidülhetnek, de csak úgy, hogy a hosszúságaik négyzeteinek összege 1 maradjon. A mérés során realizálódó két állapot az, amikor egyik vagy másik mutató hosszúsága nullává válik (theta=0 vagy theta=pí=3,14). Az egyes állapotokba való beugrás valószínűségei a mutatók hosszúságainak négyzetei – ezért kell az összegüknek 1-nek lenni.

Minden mutatóállás meghatároz egy pontot a gömbfelületen. A két mérés utáni állapot a (tetszőlegesen kijelölt) pólusoknak felel meg, például az északi sark az élet, a déli sark a halál a macska számára. Ezért mondjuk, hogy a spin fel vagy lefelé áll. Minden más köztes állapot a gömb valamelyik szélességi körén helyezkedik el. Minél északibb szélességi körön vagyunk, annál nagyobb egy mérés esetén az élet valószínűsége. "Akik élnek, azok délnek mennek, akik haldokolnak, északnak” – ahogy a Kispál énekli, de most már nem cserélem meg emiatt a pólusok szerepét az idézetnek megfelelően. Az egyenlítő pontjaiban a macska 50% valószínűséggel él vagy meghalt. Ha a két mutató szögét, a phi ún. relatív fázist változtatjuk, a valószínűség nem változik, az állapot a szélességi körön fut körbe. A relatív fázis fizikailag releváns többletinformáció a valószínűségekhez képest. Ha viszont a két vektort egyszerre forgatjuk az alpha változtatásával, sem a hosszúságaik, sem a relatív fázis nem változik, a gömbi pont nem mozdul el. A két vektor állása csak egymáshoz képest számít, az együttes elfordulásuk fizikailag irreleváns. Az állapotok gömbjét Bloch-gömbnek szokták hívni.
A harmadik ábra a Hopf-köröket mutatja a térben. Minden állapotnak megfelel egy Hopf-kör, illetve az egyik mérés utáni állapot kör helyett egyenes. Az egyre északabbra fekvő szélességi körök pontjaihoz tartozó Hopf-körök egyre dagadtabb fánkok (ún. tóruszok) felületén futnak ferdén körbe. Ez a mintázat egy négydimenziós jelenség háromdimenziós árnyéka. Az eredeti Hopf-körök a négydimenziós térben egyenlő méretűek és hiánytalanul kitöltik az ottani gömbfelületet. A tóruszok felületén tökéletes ölelésben tapad össze a kül- és a belvilág, amint azt a blogon már elmeséltem. A háromdimenziós látvány a négydimenziós mintázat kivetülése, árnyéka a közvetlenül vizualizálható világba, valahogy úgy, ahogy az alábbi GeoGebra vetület illusztrálja még eggyel kisebb dimenzió esetén. A Hopf-körökről az Érintő cikkben szólunk bővebben